Einleitung
Diese Seite handelt von der Meta-Programmierung mit C++. Aber was ist Meta-Programmierung? Bei der Meta-Programmierung geht es darum, möglichst viele Aufgaben den Compiler erledigen zu lassen. Es ist also kein Programmablauf im üblichen Sinne, sondern ein “vorberechneter” Ablauf des Compilers.
Was soll das bringen fragst sich einer. Die ganze dynamik geht verloren, kann auch ein Argument sein. Beben den herkömmlichen (prozeural, objekt orentiert) kann die Meta-Programmierung sehr viele Vorteile bringen. Da es sich um generischen Programmieren handelt, kann der Compiler dazu gebracht werden den Programmierer (noch) mehr zu unterstützen. Es ermöglicht auch mehr Möglichkeiten im Sinne der objekt orientierten Programmierung, sowie Laufzeitoptimierungen.
Diese Seite ist, obwohl auch einführende Beispiele gezeigt werden, nicht eine Einführung in die Programmierung von Templates in C++.
Als ich das Buch Modern C++ Design von Andrei Alexandrescu gelesen hatte, lernte ich viel über Templates und generisches Programmieren. Dies war auch der Auslöser diese Seite zu schreiben. Die meisten Beispiele die auf dieser Seite gezeigt werden habe ich selbst geschrieben, um mich mit der generischen Programmierung oder auch Meta-Programmierung vertraut zu machen.
Natürlich sind auf dieser Seite noch lange nicht alle Möglichkeiten enthalten, die sich durch das Gespann C++ und generisches Programmieren ergeben.
Compile-Time-Berechnungen
Dieses Kapitel zeigt wie Compile-Time Berechnungen durchgeführt werden können. Es ist keine abschliessende Liste der Möglichkeiten, soll aber zeigen, was alles möglich ist.
Minimum und Maximum
Minimum und Maximum sind eigentlich einfach zu berechnen. Wir wollen aber diese zur Compilationszeit zur Verfügung haben. Sicher ist die Möglichkeit bekannt um diesen Check Typenunabhängig durchzuführen bekannt:
template <class T> T min(T a, T b) { return (a <= b) ? a : b; }
template <class T> T max(T a, T b) { return (a >= b) ? a : b; }Dabei müssen die Operatoren <= und >= für den entsprechenden Typ verfügbar sein. Sind diese nicht, so gibt es eine alternative Implementation:
template <class T> T min(T a, T b) { return (a < b) ? a : b; }
template <class T> T max(T a, T b) { return (a > b) ? a : b; }Gleiches Problem, andere Operatoren. Diese beiden Möglichkeiten können auch kombiniert werden.
Diese benötigen allerdings Laufzeit. Wenn wir nun die gleiche Operation zur Compilationszeit durchführen wollen, müssen wir uns allerdings auf ordinale typen beschränken (int, etc.).
template <int a, int b> struct min { enum { RESULT = (a < b) ? a : b }; };
template <int a, int b> struct max { enum { RESULT = (a > b) ? a : b }; };Da es sich hier um ordinale Typen (int) handelt, sind die benötigten Operatoren vorhanden. Dies glt auch für andere orinale Typen (long, short, etc.). Leider funktioniert diese Möglichkeit nicht für Typen wie float, double und komplexe Typen.
Die Anwendung davon ist sehr einfach:
Summen
Die Summenbildung über einem bestimmten Bereich kann manchmal hilfreich sein, obwohl sicher nicht so häufig wie andere Berechnungen. Betrachten wir zuerst eine konventionelle Implementation, die eine Summe berechnet. Die folgende Funktion berechnet die Summe aller Zahlen im Interval [0,a].
Ist die Grenze a schon zur Kompilationszeit bekannt, dann können wir den Compiler anweisen diese Summe zu berechnen. Wir bedienen uns dazu dem folgenden Template:
template <int x> struct sum;
template <> struct sum<0> { enum { RESULT = 0 }; };
template <int x> struct sum { enum { RESULT = x + sum<x-1>::RESULT }; };Als Gegenüberstellung sehen wir die beiden Varianten:
Nicht wirklich verschieden, wenn es darum geht diese Anweisungen zu lesen, ihre Wirkung ist allerdings sehr verschieden.
Eine Summe über einem Bereich zu berechnen kann auch interessant werden, wenn das Intervall vergössert wird auf [a,b]. Betrachten wir zunächst wieder eine konventionelle Implementation, nehmen wir dabei an, dass a<=b gilt:
Auch diese Berechnung kann mit Hilfe des Compilers durchgeführt werden, natürlich mit den gleichen Vorbedingungen.
template <int a, int b> struct sum;
template <int b> struct sum<b,b> { enum { RESULT = b }; };
template <int a, int b> struct sum
{ enum { RESULT = a + sum<a+1,b>::RESULT }; };Eine kleine Erweiterung könnte man sich nun denken: egal welche Reihenfolge die Argumente haben, wir wollen immer die Summe berechnen. Um dieses Problem zu lösen, nehmen wir die Maximums- und Minimums-Funktion des obigen Kapitels zur Hilfe.
template <int a, int b> struct sumx;
template <int b> struct sumx<b,b> { enum { RESULT = b }; };
template <int a, int b> struct sumx
{ enum { RESULT = a + sum<a+1,b>::RESULT }; };
template <int a, int b> struct sum
{ enum { RESULT = sumx<min<a,b>::RESULT,max<a,b>::RESULT>::RESULT }; };Differenz
Eine andere nützliche Funktion ist die Differenz zweier Zahlen. Diese kann auf mehrere Arten berehnet werden, beide werden hier vorgestellt.
Zuerst die Offentsichtliche: wir haben zwei Zahlen, nehmen die Grössere und ziehen die Kleinere davon ab:
template <int a, int b> struct diffx { enum { RESULT = b-a }; };
template <int a, int b> struct diff
{ enum { RESULT = diffx<min<a,b>::RESULT,max<a,b>::RESULT>::RESULT }; };Die andere Möglichkeit basiert auf einem rekursiven Auflösen der Differenz:
template <int a, int b> struct diffx;
template <int a> struct diffx<a, a> { enum { RESULT = 0 }; };
template <int a, int b> struct diffx
{ enum { RESULT = 1 + diffx<a,b-1>::RESULT }; };
template <int a, int b> struct diff
{ enum { RESULT = diffx<min<a,b>::RESULT,max<a,b>::RESULT>::RESULT }; };Diese beiden Varianten haben, wie unschwer zu erkennen, bereits die Fähigkeit eine beliebige Reihenfolge der Argumtente zu verarbeiten.
Fakultät
Die Fakultät ist definiert als Produkt aller Zahlen zwischen 1 und a, wobei a eine ganze Zahl grösser oder gleich 1 ist.
Eine konventionelle, iterative Implementation könnte folgende Form haben:
Betrachten wir allerdings die konventionelle, rekursive Lösung:
so sind wir schon sehr viel näher an der generischen Implementation:
template <unsigned int a> struct fac;
template <> struct fac<0> { enum { RESULT = 1 }; };
template <unsigned int a> struct fac
{ enum { RESULT = a * fac<a-1>::RESULT }; };Grösster gemeinsamer Teiler
Der grösste gemeinsame Teiler, auch GGT (GCD in Englisch), ist schon ein interessanteres Beispiel als die obigen. Gegeben sind zwei ganze, positive Zahlen. Gesucht ist nun die grösste Zahl die beide ohne Rest teilen können.
template <unsigned int m, unsigned int n> struct GCD;
template <unsigned int m> struct GCD<m,0> { enum { RESULT = m }; };
template <unsigned int m, unsigned int n> struct GCD
{ enum { RESULT = GCD<n, m%n>::RESULT }; };Liste von Konstanten
Andrei hat in seinem Buch die type lists, Listen von Typen, vorgestellt. Ohne Zweifel sind diese eine geniale Sache. Um mich mit der Materie ein wenig vertraut zu machen, habe ich beschlossen eine Liste für Konstanten in ähnlicher Weise zu Implementieren. Dieses Kapitel zeigt nun das Resultat.
Das hier Berschriebene verwendet keine variadic templates wie sie ab C++11 möglich sind.
Die folgenden Unterkapitel zeigen die einzelnen Elemente die dazu verwendet werden.
Es ist durchaus denkbar, dass weitere Funktionen sinnvoll sind. Diese zu realisieren ist dem Leser überlassen.
Den gesamten Source Codes dieses Kapitels: list.cpp
Es gelten die Distributionsbestimmungen beschrieben im Anhang A.
Null Element
Als Erstes brauchen wir einen Indikator eines leeren Elementes:
Elemententasche
Um konstante Elemente, in diesem Fall ganzzahlige Werte (integer) aufzunehmen, brauchen wir einen Behälter. Dies kann auf sehr einfache Weise realisiert werden:
Zu beachten gilt es, dass die Konstante als enum definiert ist, so benötigt sie keinerlei Speicherplatz, da sie zur Compilationszeit ersetzt wird.
Die Liste
Die Liste ist genau gleich aufgebaut wie sie auch Andrei definiert hat. Sie hat ein erstes Element und einen Rest, welcher auch wieder eine Liste oder ein Null-Element sein kann.
Folgendes Beispiel definiert eine kurze Liste von Konstanten:
Vielleicht ist die Schreibweise ein wenig gewöhungsbedürtig. Dies ist ein Beispiel für den Segen der Makros:
#define LIST_1(a) list<holder< a >, null>
#define LIST_2(a,b) list<holder< a >, LIST_1(b)>
#define LIST_3(a,b,c) list<holder< a >, LIST_2(b,c)>
#define LIST_4(a,b,c,d) list<holder< a >, LIST_3(a,b,c)>Die Definition der obigen Liste wird dadurch stark vereinfacht:
Natürlich müssten für lange Listen viele Makros definiert werden. Für unsere Zwecke ist eine Liste der Länge 4 völlig ausreichend. Auffallend ist, dass die Verwendung von list immer im Zusammenhang mit holder steht. Dagegen lässt sich Nichts machen, da wir zwischen holder und null unterscheiden müssen. Eine andere, aus meiner Sicht weniger praktikable, Lösung wäre einen speziellen holder zu definieren, der das null ersetzt. Dann hätten wir die Restriktion, nicht alle Konstanten in die Liste einfügen zu können.
Nun haben wir alles was zur Infrastruktur benötigt wird. Die folgenden Unterkapitel zeigen nun die Verwendung und wie die Liste der Konstanten bearbeitet werden kann.
Länge einer Liste
Oft ist es interessant zu erfahren, wie viele Elemente sich in einer Liste befinden. Tatsächlich ist dies sehr einfach realisieren:
template <class list> struct length;
template <> struct length<null> { enum { value = 0 }; };
template <class h, class t> struct length<list<h,t> >
{ enum { value = 1+length<t>::value }; };Dies ist nichts Anderes als ein rekursives hangeln durch die Liste und jeweils das Resultat anzupassen. Die Anwendung gestaltet sich denkbar einfach:
Werte
Die Liste wäre Nutzlos, könnten wir nicht die Werte aus der Liste auslesen. Diese Möglichkeit bietet uns valueat:
template <class list, unsigned int i> struct valueat;
template <unsigned int i> struct valueat<null,i>
{ enum { value = 0 }; };
template <class h, class t> struct valueat<list<h,t>,0>
{ enum { value = h::value }; };
template <class h, class t, unsigned int i> struct valueat<list<h,t>,i>
{ enum { value = valueat<t,i-1>::value }; };Die Liste wird solange durchschritten (und der Index dekrementiert), bis der Index auf die Abbruchbedingung (gleich 0) stösst. Dort befindet sich der gesuchte Wert. Falls der Index ausserhalb der Liste liegt, wird 0 zurückgeliefert.
Die Anwendung ist sehr einfach, wir haben ja nichts Anderes erwartet:
Indices
Die umgekehrte Operation von valueat liefert den Index des gegebenen Wertes. Fall mehrere gleiche Werte in der Liste vorkommen, so wird immer der kleinste Index zurückgeliefert. Dies ist die Aufgabe von indexof:
template <class list, class item> struct indexof;
template <class item> struct indexof<null,item>
{ enum { value = -1 }; };
template <class t, class item> struct indexof<list<item,t>,item>
{ enum { value = 0 }; };
template <class h, class t, class item> struct indexof<list<h,t>,item>
{
private: enum { temp = indexof<t,item>::value };
public: enum { value = (temp == -1) ? -1 : 1 + temp };
};Sehr einfach können nun Indices von Werten ermittelt werden, jedoch müssen wir wieder auf die Verwendung von holder zurückgreifen:
Das Auslesen eines Indexes bietet uns noch eine andere Anwendung. Es ist möglich unter der Verwendung von indexof die Länge der Liste zu ermitteln:
Die Läge der Liste ist also der Index des abschliessenden Null-Elements.
indexof ist genügend robust um auch Dinge auszuhalten wie null Listen:
liefert -1.
Löschen aus der Liste
Hin und wieder kann es vorkommen, dass nicht die gesamte Liste benötigt wird. Es ist vorstellbar, dass ein einzelnes Element aus der Liste entfernt werden soll.
template <class list, class item> struct erase;
template <class item> struct erase<null,item>
{ typedef null result; };
template <class item, class t> struct erase<list<item,t>,item>
{ typedef t result; };
template <class h, class t, class item> struct erase<list<h,t>,item>
{ typedef list<h,typename erase<t,item>::result> result; };Das angegebene Element wird aus der Liste gelöscht. Falls es mehrere gleiche Elemente in der Liste gibt, so wird immer das erste gelöscht. Es ist nicht möglich, das letzte Element null zu löschen.
Löschen der Liste
Wenn ein einzelnes Element gelöscht werden kann, dann auch die ganze Liste. Geeignete Einsatzmöglichkeiten wollen mir jetzt gerade nicht einfallen, aber ist ist möglich.
template <class list, class item> struct eraseall;
template <class item> struct eraseall<null,item>
{ typedef null result; };
template <class item, class t> struct eraseall<list<item,t>,item>
{ typedef typename erase<t,item>::result result; };
template <class h, class t, class item> struct eraseall<list<h,t>,item>
{ typedef list<h,typename eraseall<t,item>::result> result; };Löschen von Duplikaten aus der Liste
Das Löschen von Duplikaten hat gegenüber von eraseall eine sehr grosse bedeutung. Es kann durchaus sein, dass eine Liste Duplikate aufweist, jedoch in gewissen Fällen nicht erwünscht ist.
template <class list> struct erasedup;
template <> struct erasedup<null>
{ typedef null result; };
template <class h, class t> struct erasedup<list<h,t> >
{
private: typedef typename erasedup<t>::result tmp1;
private: typedef typename erase<tmp1,h>::result tmp2;
public: typedef list<h,tmp2> result;
}Die Anwendung ist zwar trivial aber Vollständigkeitshalber hier aufgeführt:
Element Ersetzen
Ein einzelnes Element zu ersetzen kann auch ein Wunsch sein. Hier geht er in Erfüllung. Das abschliessende Element null kann nicht ersetzt werden. Falls die Liste Duplikate aufweist, so wird immer das zuerst gefundene Element ersetzt.
template <class list, class f, class r> struct replaceitem;
template <class f, class r> struct replaceitem<null,f,r>
{ typedef null result; };
template <class f, class t, class r> struct replaceitem<list<f,t>,f,r>
{ typedef list<r,t> result; };
template <class h, class t, class f, class r> struct replaceitem<list<h,t>,f,r>
{ typedef list<h,typename replaceitem<t,f,r>::result> result; };Die Anwendung:
zeigt, wie das Element 20 durch 25 ersetzt wird, so dass eine neue Liste bar entsteht mit Inhalt {10,25,30}.
Alle Elemente Ersetzen
Analog zu replaceitem ersetzt replaceall alle Duplikate in einer Liste. Das abschliessende Element null kann nicht ersetzt werden.
template <class list, class f, class r> struct replaceall;
template <class f, class r> struct replaceall<null,f,r>
{ typedef null result; };
template <class f, class t, class r> struct replaceall<list<f,t>,f,r>
{ typedef list<r,typename replaceall<t,f,r>::result> result; };
template <class h, class t, class f, class r> struct replaceall<list<h,t>,f,r>
{ typedef list<h,typename replaceall<t,f,r>::result> result; };Beispiel:
Die Liste two ist nun: {5,6,5,8}.
Ganze Liste Drucken
Zur einfacheren Ausgabe von Listen bedienen wir uns folgendem Konstrukt. Es sollte kaum erwähnenswert sein, dass diese Ausgabe natürlich nicht zur Kompliationszeit erfolgen kann.
template <class list> struct show
{};
template <> struct show<null>
{ static void print(ostream &) {} };
template <class h> struct show<list<h,null> >
{ static void print(ostream & os) { os << h::value; } };
template <class h, class t> struct show<list<h,t> >
{
static void print(ostream & os)
{ os << h::value << ","; show<t>::print(os); }
};Die Ausgabe auf cout kann dann einfach durch den folgenden Aufruf erfolgen:
Maximum der Liste ermitteln
Das Maximum der Liste kann relativ einfach ermittelt werden. Jedoch wird keine Prüfung auf mehrere Maxima durchgeführt.
template <class list> struct max_of;
template <> struct max_of<null>
{ enum { value = 0 }; };
template <class t> struct max_of<list<t,null> >
{ enum { value = t::value }; };
template <class h, class t> struct max_of<list<h, t> >
{
private: enum { tmp1 = max_of<t>::value, tmp2 = h::value };
public: enum { value = (tmp1 > tmp2) ? tmp1 : tmp2 };
};Das Maximum wird ermittelt mit:
Minimum der Liste ermitteln
Analog zu max_of kann auch das Minimum gefunden werden.
template <class list> struct min_of;
template <> struct min_of<null>
{ enum { value = 0 }; };
template <class t> struct min_of<list<t,null> >
{ enum { value = t::value }; };
template <class h, class t> struct min_of<list<h, t> >
{
private: enum { tmp1 = max_of<t>::value, tmp2 = h::value };
public: enum { value = (tmp1 < tmp2) ? tmp1 : tmp2 };
};Das Maximum wird ermittelt mit:
Listen
Nebst allen Einsatzmöglichkeiten von generischem Programmieren um möglichst viel zur Compilationszeit zu erledigen, gibt es auch sehr interessante und brauchbare Ansätze für das Design.
Dieses Kapitel stellt nun drei verschiedene Designs und Implementationen von spezialisierten Listen (Stack und Queue) vor. Die erste Variante in konventionellem objektorientiertem Ansatz mit dynamischer Bindung. Die zweite Variante mit halb generischer Implementation und dynamischer Bindung. Die dritte mit generischer Programmierung und statischer Bindung. Vor- und Nachteile hängen vom konkreten Einsatz ab.
Objektorientiert
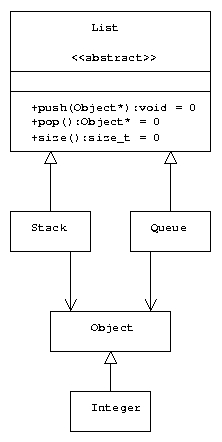
Source code mit Demo: objectoriented.cpp
Es gelten die Distributionsbestimmungen beschrieben im Anhang A.
Vorteile:
- Implementierbar in Sprachen die keine generischen Konstrukte kennen.
- Dynamische Bindung kann sehr nützlich sein. In diesem Anwendungsfall von Listen, wird diese allerdings nicht häufig benötigt.
Nachteile:
- Nicht type-safe. Ein type-casting ist immer nötig um die richtigen Typen zu bekommen.
- Alle Objekte von Klassen die in einer solchen Liste verwaltet werden müssen zwingend immer von Object abgeleitet werden. Primitive Typen können nicht verwaltet werden.
- Methoden haben zum Teil gleiche Implementation, z.B.
pop(), und können trotzdem nicht zusammengefasst werden. Dieser Fall kann auftreten, wenn ausser Stack und Queue noch andere Klassen von List erben sollen. Eine solche Codevervielfältigung sollte vermieden werden, ist allerdings nicht immer möglich.
Auf spezifische Punkte/Erklärungen bezüglich des Source Codes wird an dieser Stelle nicht näher eingegangen.
Semi-Generisch
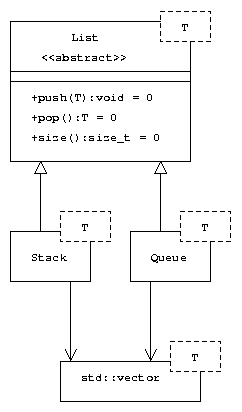
Source code mit Demo: semigeneric.cpp
Es gelten die Distributionsbestimmungen beschrieben im Anhang A.
Vorteile:
- Dynamische Bindung kann sehr nützlich sein. In diesem Anwendungsfall von Listen, wird diese allerdings nicht häufig benötigt.
- Alle erdenkbaren Typen können verwaltet werden, auch primitive Typen.
- Type-safe
Nachteile:
- Wie beim objektorientierten Ansatz gibt es auch hier multiplikationen von Code.
Auf spezifische Punkte/Erklärungen bezüglich des Source Codes wird an dieser Stelle nicht näher eingegangen.
Generisch
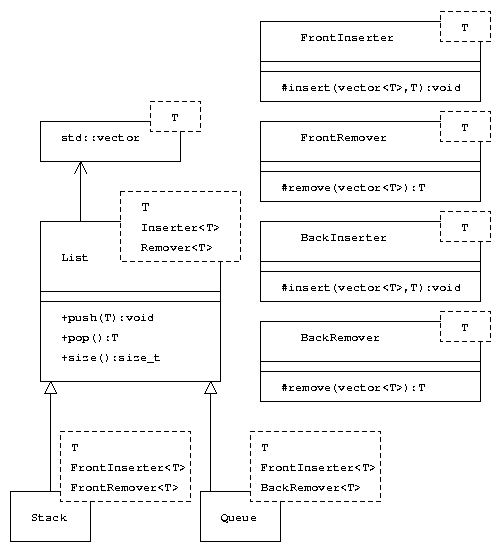
Source code mit Demo: generic.cpp
Es gelten die Distributionsbestimmungen beschrieben im Anhang A.
Vorteile:
- Alle erdenkbaren Typen können verwaltet werden, auch primitive Typen.
- Type-safe
- Keine multiplikation von Code. Die übernimmt der Compiler.
- Keine Laufzeitverzögerung, da keine v-table benötigt.
Nachteile:
- Statische Bindung kann hinderlich sein. In diesem Anwendungsfall von Listen, wird allerdings eine dynamische Bindung nicht häufig benötigt.
Beschreibung
Es existieren die vier generische Klassen
BackInserterFrontInserterBackRemoverFrontRemover
die jeweils eine Strategie implementieren um Daten in einen vector zu schreiben, bzw. zu entfernen. Die generische Klasse List, übernimmt zwei Strategien um von ihnen zu erben. Wichtig sind die Methoden, also die jeweiligen Implementationen, die vererbt werden:
template <
class T,
template <class T> class Inserter,
template <class T> class Remover
>
class List : public Inserter<T>, public Remover<T>Der Trick daran ist nun, dass mit Hilfe der Vererbung von List nach Stack bzw. Queue die jeweiligen Strategien definiert werden können. Dabei muss kein Code vervielfältigt werden:
template <class T> class Stack : public List<T,FrontInserter,FrontRemover> {};
template <class T> class Queue : public List<T,FrontInserter,BackRemover> {};Der Vorteil liegt hier klar auf der Hand: es ist nun sehr einfach weitere Strategien für insert und remove zu implementieren und diese dann wieder einzusetzen in einer weiteren von abgeleiteten List Klasse.
Erweiterungsmöglichkeiten wären z.B. eine Strategie die eine Sortierreihenfolge der Elemente erzwingt. Auch die Sortiermethode könnte als Strategie dazukommen. Diese Erweiterungen sind dem geneigten Leser überlassen.
Nebst allen Vorteilen, wie auch oben schon aufgeführt, gibt es auch den Nachteil nicht dynamisch binden zu können. In diesem Fall ist das nicht weiter schlimm, da typischerweise die Logik eines Programmablaufs verändert werden muss um von einem Stack auf eine Queue umschalten zu müssen. Falls doch sollte vielleicht eher auf eine der beiden andern Ansätze zurückgegriffen werden.
Auf einen weitern Code-Walkthrough wird an dieser Stelle verzichtet.
Anhang A: Source Codes
Alle Source Codes auf dieser Seite sind frei zu kopieren, zu verändern, weiterzuverbreiten, zu verwenden oder in sonstiger Weise zu verwenden. Die Übersetzung und Ausführung der Programme geschieht auf eigenes Risiko. Jegliche Haftung wird abglehnt. Das Copyright liegt bei Mario Konrad.
Makefile:
# This file is free to copy, modify, distribute or to use in any manner.
# Use it on your own risk. Copyright by Mario Konrad.
CC=gcc
CXX=g++
CXXLIBS=-lstdc++
CXXFLAGS=-O2 -Wall
all: generic objectoriented semigeneric list
generic: generic.o
$(CXX) -o $@ $^ $(CXXLIBS)
generic-clean:
find . -maxdepth 1 -name "generic" -exec rm -fr {} \;
objectoriented: objectoriented.o
$(CXX) -o $@ $^ $(CXXLIBS)
objectoriented-clean:
find . -maxdepth 1 -name "objectoriented" -exec rm -fr {} \;
semigeneric: semigeneric.o
$(CXX) -o $@ $^ $(CXXLIBS)
semigeneric-clean:
find . -maxdepth 1 -name "semigeneric" -exec rm -fr {} \;
list: list.o
$(CXX) -o $@ $^ $(CXXLIBS)
list-clean:
find . -maxdepth 1 -name "list" -exec rm -fr {} \;
clean: \
generic-clean \
semigeneric-clean \
objectoriented-clean \
list-clean
find . -maxdepth 1 -name "*~" -exec rm -fr {} \;
find . -maxdepth 1 -name "*.bak" -exec rm -fr {} \;
find . -maxdepth 1 -name "*.exe" -exec rm -fr {} \;
find . -maxdepth 1 -name "*.o" -exec rm -fr {} \;
.cpp.o:
$(CXX) -o $@ -c $< $(CXXFLAGS)